8.Sınıf LGS Hazırlık Çarpanlar ve Katlar Konu Anlatımı+Video LGS-ÇARPANLAR VE KATLAR-KONU ANLATIMI-VİDEO-TESTBir Tam Sayının Çarpanları Bir doğal sayı, birden fazla doğal sayının çarpımı şeklinde yazılabilir. Bu doğal sayıların her birine o sayının çarpanı denir. Bir doğal sayının çarpanı aynı zamanda o sayının bölenidir.→ 36 sayısının çarpanlarını bulalım. 36= 1.36 36= 2.18 36= 3.12 36= 4.9 36= 6.6 Bu durumda 36’nın çarpanları; 1,2,3,4,6,9,12,18 ve 36’dır. → 36 sayısının bölenlerini bulalım. 36:1= 36 36:2= 18 36:3= 12 36:4= 9 36:6= 6 36:9= 4 36:12= 3 36:18= 2 36:36= 1 Bu durumda 36’nın bölenleri; 1,2,3,4,6,9,12,18 ve 36’dır. Yukarıda da gördüğümüz gibi bir sayının çarpanı ve böleni birbiriyle aynıdır. NOT: • Her tam sayı kendisinin çarpanıdır. • 1 Bütün sayıların çarpanıdır. ÖRNEK: Alanı 32 cm2 olan bir dikdörtgenin çevre uzunluğu kaç santimetre olabilir? ÇÖZÜM: Dikdörtgenin alanı kısa kenarı ile uzun kenarının çarpımına eşittir. O halde kısa ve uzun kenarlarının uzunluğunu bulabilmek için çarpımı 32 olan sayıları bulalım. 32= 1.32 32= 2.16 32= 4.8 Bu durumda alanı 32 cm2 olan üç dikdörtgen çizilebilir. 1. Dikdörtgen; Kısa kenarı: 1 Uzun kenarı: 32 Çevresi= 66 2. Dikdörgen; Kısa kenarı: 2 Uzun kenarı: 16 Çevresi= 36 3. Dikdörtgen; Kısa kenarı: 4 Uzun kenarı: 8 Çevresi= 24 Asal Sayı Kendisi ve 1 dışında pozitif çarpanı olmayan sayılara asal sayı denir. DİKKAT! → 1 asal sayı değildir. → En küçük asal sayı 2’dir. → 2 dışında çift asal sayı yoktur. Aşağıda verilen tabloda 0’dan 100’e kadar olan asal sayılar verilmiştir. 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61, 67,71,73,79,83,89 ve 97 sayıları asal sayıdır. SEN YAP: → Aşağıdaki boşlukları doldurunuz. • En küçük asal sayı ............’dır. • İki basamaklı en küçük asal sayı ..............’dir. • İki basamaklı en büyük asal sayı ..............’dir. • Birler basmağı 4 olan ....... tane iki basamaklı asal sayı vardır. → Birler basamağı 3 olan iki basamaklı asal sayıların toplamı kaçtır? → İki basamaklı a7 sayısı asal sayı olduğuna göre a’nın alacağı değerler toplamı kaçtır? Asal Çarpanlar Bir doğal sayının pozitif çarpanları arasında asal sayı olanlara asal çarpan denir. → 36 sayısının çarpanları; 1,2,3,4,9,12,18 ve 36’dır. 36 sayısının asal çarpanları; 2 ve 3’tür. SEN YAP: →Aşağıdaki sayıların asal çarpanlarını bulunuz. • 18= • 24= • 30= • 42= • 48= Asal çarpanları daha kolay bir şekilde bulabilmek için verilen sayıyı tam bölünebilen en küçük asal sayıdan başlayarak sırasıyla bölme yapılır. Buna asal çarpanlara ayırma denir Asal çarpanlara ayırmak için iki yöntem vardır; 1-) Çarpan Ağacı Yöntemi 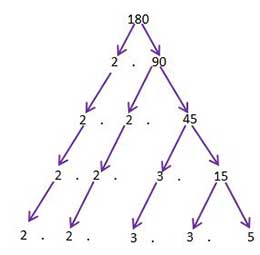 180=2.2.3.3.5 asal çarpanları 2,3 ve 5'tir. 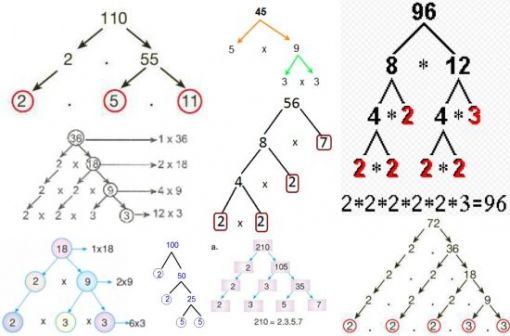 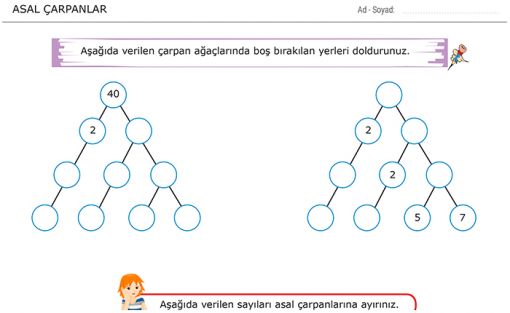 2-) Asal Çarpan Algoritması   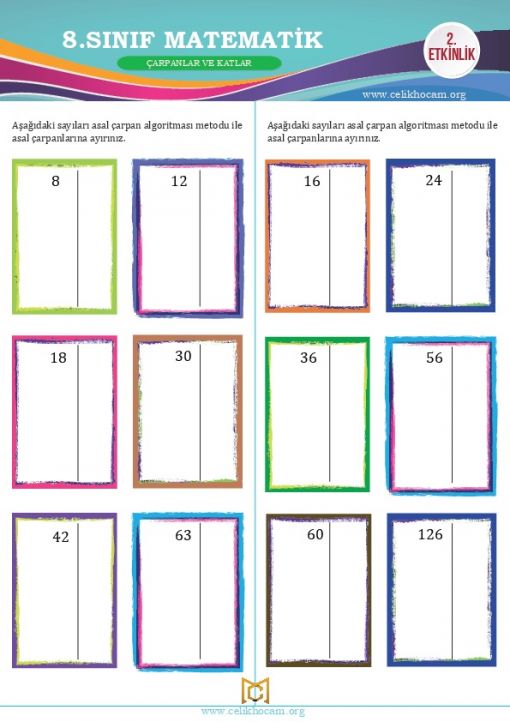 EKOK (En Küçük Ortak Kat) İki veya daha fazla sayının ortak katlarının en küçüğüne en küçük ortak kat EKOK denir. Örnek: 3→ 3, 6, 9, 12, 18, 21, 24, 27… 12→ 12, 24, 48 … 3 ve 12 sayılarının 12, 24, 48 … gibi bir çok ortak katı vardır. Bu ortak katların arasında en küçük ortak katları 12’dir. EKOK bulunurken verilen sayıların tümü yan yana yazılır ve bir olana kadar asal sayılarla bölünür.En sonunda da asal çarpanların tümü birlikte çarpılır. 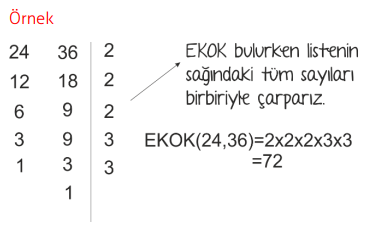 *Biri diğerinin katı olan iki sayıdan büyük olanı EKOK’a eşittir. Örnek: EKOK (6, 24) = 24 *Ortak asal çarpanların üssü en büyük olanlar ile ortak olmayanların çarpımı ile de EKOK bulunur. Örnek: 48, 54, 60 sayılarının en küçük ortak katları kaçtır?  => Problemlerde küçük parçalardan büyük parçalara geliyorsa yani elde ediliyorsa EKOK bulunarak çözüme gidilir. =>EKOK ile çözülen problemler genellikle şu şekildedir; >Birtakım nesneler (ceviz, top, boncuk) vesaire sayılıyor ve sayıldıktan sonra artan oluyorsa >Aynı anda harekete başlayan arabalar belirli bir süre sonra tekrar karşılaşması süreleri soruluyorsa >Küçük küplerden veya dikdörtgenler prizmasından büyük bir küp yapılması isteniyorsa >Nöbet, gün, alarm gibi aynı anda başlayan durumların birlikte tekrar-lanmaları soruluyorsa >Sıralara oturan öğrenciler de ayak-ta kalan oluyorsa gibi sorulardır. Örnek: Kavanozdaki cevizler ikişerli altışarlı ve dokuzarlı paylaştıklarında her seferinde bir ceviz artmaktadır. Buna göre sepette en az kaç ceviz vardır? Çözüm: İlk olarak 2, 6 ve 9 sayılarının en küçük ortak katlarını bulmamız gerekir. EKOK (2, 6, 9) = 18 Eğer 18 ceviz olsaydı; ikişerli, altışarlı ve dokuzarlı paylaştıklarında hiç ceviz artmayacaktı. Fakat soru da her seferinde 1 ceviz arttığını söylediği için artan cevizi sonuca eklemeliyiz. 18+1 = 19 kavanozdaki ceviz sayısı. Örnek: Boyutları 25cm ve 15cm olan olan dikdörtgen şeklindeki fayanslarla kaplanabilecek en küçük karenin alanı kaç cm2 ' dir? Çözüm: İlk olarak 25 ve 15 sayılarının en küçük ortak katlarını bulmamız gerekir. EKOK (15, 25) = 3. 5 2=75 Oluşabilecek en küçük karenin alanı 75 cm2 ’dir. EBOB (En Büyük Ortak Bölen) İki veya daha fazla sayının ortak bölenlerinin en büyüğüne en büyük ortak bölen EBOB denir. Örnek: 48→ 1, 2, 3, 4, 6, 8, 12, 24, 48 36→ 1, 2, 3,4, 6, 9, 12, 18, 36 48 ve 36 sayılarını bölebilen sayılar yukarıdaki gibidir. Bu sayıları ortak bölebilen sayıların arasında en büyük ortak bölen 12’dir. EBOB bulunurken verilen sayıların tümü yan yana yazılır ve bir olana kadar asal sayılarla bölünür.Bu işlem yapılırken her iki sayıyı da ortak bölebilen asal sayıları unutmamak için bu sayıların köşesine yıldız koymanızda fayda var. En sonunda da ortak bölen asal sayıların tümü birlikte çarpılır. 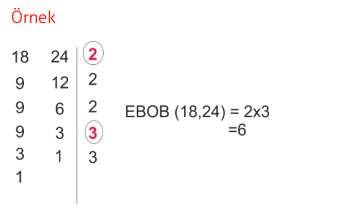 *Biri diğerinin katı olan iki sayıdan küçük olanı EBOB’e eşittir. Örnek: EBOB (6, 24) = 6 *Ortak asal çarpanların üssü küçük olanların çarpımı ile de EBOB bulunur. (Ortak olmayan çarpan alınmaz.) Örnek: 48, 54, 60 sayılarının en büyük ortak böleni kaçtır?  => Problemlerde büyük parçalardan küçük parçalara gidiliyorsa yani elde ediliyorsa EBOB bulunarak çözüme gidilir. =>EBOB ile çözülen problemler genellikle şu şekildedir; >Tahta ve kumaş gibi nesnelerin parçalara ayrılması >Dikdörtgen şeklinden küçük kare şekiller elde etmek >Bir bölgenin etrafına eşit aralıklarla dikilebilecek ağaç ve direk sayıları >Çuvallarda şişelerde bulunan malzeme ve sıvıların başka kaplara aktarılması gibi sorular EBOB ile çözülür. Örnek: Kenar uzunlukları 18 ve 30 cm olan dikdörtgen şeklindeki bir karton eşit alanlı karelere ayrılmak isteniyor. Bu iş için en az kaç karton gerekir?  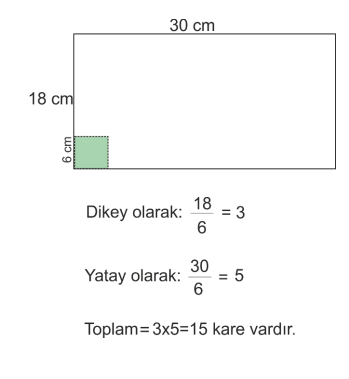  Kaynak: mehmethocaniz.com Çarpanlar ve Katlar poster indir : (resme tıkla)  Çarpanlar ve Katlar Test indir 1 Çarpanlar ve Katlar Test indir 2 Çarpanlar ve Katlar Test indir 3 Çarpanlar ve Katlar Test indir 4 LGS Çarpanlar ve Katlar Çıkmış Sorular İndir. Kaynak:www.matematikciler.com 8. sınıf çarpanlar ve katlar konusu sekizinci sınıf 1. ünitenin ilk konusudur. Bu konuda 6. sınıfta öğrendiğiniz bilgileri tazeleyecek ve bir adım ileri götüreceksiniz. Çarpan ve asal çarpan bulma, ebob – ekok, aralarında asal sayılar bu konudaki alt konular. |
|
3131 kez okundu
YorumlarHenüz yorum yapılmamış. İlk yorumu yapmak için tıklayın |