LGS

Konu Anlatımları

Videolar

Instagram Sayfamız

Takvim

8.Sınıf LGS Hazırlık Cebirsel İfadeler ve Özdeşlikler Konu Anlatımı+Video

LGS-CEBİRSEL İFADELER VE ÖZDEŞLİKLER-KONU ANLATIMI-VİDEO

8. sınıf cebirsel ifadeler ve özdeşlikler konusu sekizinci sınıf 3. ünitenin 2. konusudur. Cebirsel ifadeleri seven de var sevmeyen de ancak bundan sonraki eğitim hayatınızda önemli bir yer kaplayacağından şüpheniz olmasın.Cebirsel ifadeler ve özdeşlikler konu anlatımı 4 başlık halinde hazırlanmıştır. Konulardan daha fazla verim almak için aşağıdaki konu başlıklarını sırasıyla okuyunuz ve her konunun sonunda verilen kazanım testlerini çözünüz. İyi çalışmalar…

CEBİRSEL İFADELER

CEBİRSEL İFADE VE BİLİNMEYEN NEDİR?

En az bir bir bilinmeyen ve bir işlem içeren ifadelere cebirsel ifadeler denir. Cebirsel ifadelerde sayıları temsil eden harflere değişken ya da bilinmeyen denir.

ÖRNEK : Bir sayının 2 katının 3 fazlası ifadesini cebirsel ifade olarak yazalım.

Cebirsel ifademiz: 2x + 3 olur. Bu cebirsel ifadede “x” bilinmeyendir.

TERİM VE KATSAYI NEDİR?

Bir cebirsel ifadede bir sayı ile bir veya birden fazla değişkenin çarpımına terim denir. Terimlerde çarpım durumunda bulunan sayıya katsayı denir.

ÖRNEK : 5x ifadesinde x bilinmeyen, 5 ise katsayıdır.

Terimleri birbirinden ayırmak için “+” ve “−” sembollerinin önünden ifadeyi böleriz. Her parça bir terimdir.

ÖRNEK : 5x + 2y − 7 ifadesini inceleyelim.

5x + 2y − 2 ifadesini “+” ve “−” işaretlerinin önünden bölersek terimleri elde ederiz.

5x / + 2y / − 7 ifadesi 3 terimlidir. Terimleri 5x, 2y ve −7’dir

SABİT TERİM NEDİR?

İçerisinde değişken bulunmayan terime sabit terim denir.

ÖRNEK : 6y + 12 ve −3x − 9 ifadelerinde sabit terimleri bulalım.

6y + 12 cebirsel ifadesinde sabit terim +12’dir.

−3x − 9 cebirsel ifadesinde sabit terim −9’dur.

Sabit terim de bir katsayıdır.

5x² − 7 cebirsel ifadesinde kat sayılar 5 ve −7’dir.

CEBİRSEL İFADELERDE ÇARPMA İŞLEMİ

Cebirsel ifadelerle çarpma işlemi yapılırken çarpanlardan birindeki her bir terim ile diğerindeki her bir terim ayrı ayrı çarpılır. Elde edilen sonuçta benzer terimler varsa bunlar arasında toplama çıkarma işlemi yapılarak sadeleştirme yapılır.

1 Terimli ile 1 Terimli Cebirsel İfadeyi Çarpma

Katsayılar çarpılıp katsayı olarak, bilinmeyenler çarpılıp bilinmeyen olarak sonuca yazılır.

ÖRNEK : 6 ifadesi ile 2x ifadesini çarpalım.

6 ile 2x’in katsayısı (2) çarpılır. 6.2=12

Bilinmeyen olarak sadece x olduğu için sonuç 12x bulunur.

ÖRNEK : 3x ifadesi ile 5x ifadesini çarpalım.

3x’in katsayısı (3) ile 5x’in katsayısı (5) çarpılır. 3.5=15

3x’teki bilinmeyen (x) ile 5x’teki bilinmeyen (x) çarpılır. x.x=x2

Sonuç: 3x.5x = 15x²

ÖRNEK : −4x ile 2y’i çarpalım

Katsayılar çarpımı: −4.2=−8

Biinmeyenler çarpımı: x.y = xy

−4x . 2y = −8xy

1 Terimli ile 2 Terimli Cebirsel İfadeyi Çarpma

Bir terimlideki terim diğer iki terimle sırayla çarpılır ve en son varsa sadeleştirme yapılır.

ÖRNEK : 5 . ( 7x + 2y ) işlemini yapalım.

Tek terimli 5, diğer iki terimle ayrı ayrı çarpılır. (Dağılma Özelliği)

= 5 . 7x + 5 . 2y

= 35x + 10y

ÖRNEK : −2x . ( x + 3 ) işleminde de aynı şekilde x ve +3’ü sırayla −2x ile çarparız.

= ( −2x . x) + ( −2x . 3 )

= (−2x²) + (−6x)

2 Terimli ile 2 Terimli Cebirsel İfadeyi Çarpma

İlk çarpandaki her bir terim ile ikinci çarpandaki her bir terim ayrı ayrı çarpılır. Sonra sadeleştirme varsa yapılır.

ÖRNEK : ( 2x + 3 ) . ( 4x + 1 ) işlemini yapalım.

İlk ifadedeki 2x’i diğer ifadedeki 4x ve +1 ile ayrı ayrı çarpacağız.

Benzer şekilde ilk ifadedeki +3’ü diğer ifadedeki 4x ve +1 ayrı ayrı çarpacağız.

= (2x.4x) + (2x.+1) + (3.4x) + (+3.+1)

= 8x² + 2x + 12x + 3 [2x ile 12x toplanır]

= 8x² + 14x + 3

ÖRNEK : ( x − 1 )2 işlemini yapalım.

( x − 1 )² = ( x − 1 ) . ( x − 1 ) demektir.

Önce ilk ifadedeki x ile diğer ifadedeki x ve −1 çarpılır.

Sonra ilk ifadedeki −1 ile diğer ifadedeki x ve −1 çarpılır.

= (x.x) + (x.−1) + (−1.x) + (−1.−1)

= x² + (−x) + (−x) + 1 [−x ile −x toplanır]

= x² −2x +1

ÖZDEŞLİK NEDİR?

İçindeki değişkenlere verilen bütün gerçek sayılar için doğru olan denklemlere özdeşlik denir.

ÖZDEŞLİK Mİ DENKLEM Mİ?

Özdeşlik mi denklem mi demek aslında kafaları karıştıran bir ifade çünkü özdeşlikler de aynı zamanda denklemdir. “Özdeşlik mi? Özdeşlik değil mi?” sorusu daha uygun bir soru olabilir. Özdeşlik ile denklem arasındaki fark; özdeşlikte değişkene verilen her gerçek sayı değerinde eşitlik sağlanır, denklemde ise bazı gerçek sayı değerlerinde eşitlik sağlanır.(Buradaki denklemden kasıt özdeşlik olmayan denklemdir.)

ÖRNEK: 2.(x − 2) = 2x − 4 ve 2.(x − 2) = 4 eşitliklerinde x yerine farklı değerler vererek eşitliğin sağlanıp sağlanmadığını kontrol edelim.

x yerine her iki eşitlikte de 1 yazalım

2.(x − 2) = 2x − 4
2.(1 − 2) = 2.1 − 4
−2 = −2

2.(x − 2) = 4
2.(1 − 2) = 4
−2 ≠ 4

x yerine her iki eşitlikte de 2 yazalım

2.(x − 2) = 2x − 4
2.(2 − 2) = 2.2 − 4
0 = 0

2.(x − 2) = 4
2.(2 − 2) = 4
0 ≠ 4

x yerine her iki eşitlikte de 4 yazalım

2.(x − 2) = 2x − 4
2.(4 − 2) = 2.4 − 4
4 = 4

2.(x − 2) = 4
2.(4 − 2) = 4
4 = 4

Görüldüğü gibi soldaki eşitlik x yerine yazdığımız üç değer için de sağlandı. Sağdaki eşitlik ise x yerine sadece 4 yazdığımızda sağlandı. Bu yüzden: 2.(x − 2) = 2x − 4 bir özdeşlikti, 2.(x − 2) = 4 özdeşlik değildir.

# Bir eşitliğin özdeşlik olup olmadığını anlamak için farklı değerler verip eşitliğin sağlanıp sağlanmadığına bakılabilir. Eğer verilen tüm değerler için sağlamıyorsa özdeşlik değildir.

# Bir eşitliğin özdeşlik mi denklem mi olduğunun ikinci yolu ise denklemi çözmektir. Eğer denklemi çözdükten sonra 0=0 çıkıyorsa bu denklem bir özdeşliktir.

ÖRNEK: 3x − 5 = x + 3 ve 2x + 2 = 2 + 2x eşitliklerinden özdeşlik olanlarını belirleyelim.

Önce ilk denklemi çözelim.

3x − 5 = x + 3
3x − x = 3 + 5
2x = 8
x = 4

İlk eşitlik özdeşlik değildir. (Sadece x=4 için eşitlik sağlanır.)

Şimdi ikinci denklemi çözelim.

2x + 2 = 2 + 2x
2x − 2x = 2 − 2
0 = 0

İkinci eşitlik bir özdeşliktir. (x’in her değeri için eşitlik sağlanır.)

ÖNEMLİ ÖZDEŞLİKLER

TAM KARE ÖZDEŞLİĞİ – İKİ TERİMİN TOPLAMININ KARESİ

İki terimin toplamının karesi, bu iki terimin kareleri ve bu iki terimin çarpımının iki katının toplamına eşittir.
(a + b)² = a² + 2ab + b²

ÖRNEK: Bu özdeşliği şu şekilde kullanabiliriz. 102’nin karesini bu özdeşlik sayesinde şu şekilde bulabiliriz.

(100 + 2)² = 100² + 2.100.2 + 2²
(100 + 2)² = 10000 + 400 + 4
(100 + 2)² = 10404

TAM KARE ÖZDEŞLİĞİ – İKİ TERİMİN TOPLAMININ KARESİNİ MODELLEME

Birinci şekildeki karenin alanı, parçaların alanları toplamına eşittir.

TAM KARE ÖZDEŞLİĞİ – İKİ TERİMİN FARKININ KARESİ

İki terimin farkının karesi, bu iki terimin kareleri toplamından bu iki terimin çarpımının iki katının çıkarılmasına eşittir.
(a − b)² = a² − 2ab + b²

ÖRNEK: Bu özdeşliği şu şekilde kullanabiliriz. 97’nin karesini bu özdeşlik sayesinde şu şekilde bulabiliriz.

(100 − 3)² = 100² − 2.100.3 + 3²
(100 − 3)² = 10000 − 600 + 9
(100 − 3)² = 9409

TAM KARE ÖZDEŞLİĞİ – İKİ TERİMİN FARKININ KARESİNİ MODELLEME

Birinci şekildeki yeşil karenin alanı, büyük karenin alanından beyaz bölgelerin alanlarının çıkarılmasına eşittir.

İKİ KARE FARKI ÖZDEŞLİĞİ

İki terimin karelerinin farkı, bu iki terimin toplamı ile farkının çarpımına eşittir.
a² − b² = (a − b) . (a + b)

ÖRNEK: Bu özdeşliği şu şekilde kullanabiliriz. 75’in karesi ile 25’in karesinin farkını bu özdeşlik sayesinde şu şekilde bulabiliriz.

75² − 25² = (75 − 25) . (75 + 25)
75² − 25² = 50 . 100
75² − 25² = 5000

İKİ KARE FARKI MODELLEME

Birinci şekildeki büyük kareyle küçük karenin alanları farkı (sarı bölge), ikinci şekildeki sarı bölgeye eşittir.

BİR KAÇ ÖNEMLİ ÖZDEŞLİK

İKİ KARE FARKI

a² − b² = (a − b) . (a + b)

İKİ KARE TOPLAMI

a² + b² = (a − b)² + 2ab

a² + b² = (a + b)² − 2ab

TAM KARE İFADELER

(a + b)² = a² + 2ab + b²

(a − b)² = a² − 2ab + b²

(a + b)² = (a − b)² + 4ab

(a − b)² = (a + b)² − 4ab

İKİ KÜP FARKI

a³ − b³ = (a − b) . (a2 + ab + b2)

a³ + b³ = (a + b) . (a2 − ab + b2)

a³ − b³ = (a − b)³ + 3ab . (a − b)

a³ + b³ = (a + b)³ − 3ab . (a + b)

KÜP AÇILIMI

(a + b)³ = a³ + 3a²b + 3ab² + b³

(a − b)³ = a³ − 3a²b + 3ab² − b³

CEBİRSEL İFADELERİ ÇARPANLARA AYIRMA

Bir cebirsel ifadeyi çarpanlarının çarpımı şeklinde yazmaya, o cebirsel ifadeyi çarpanlara ayırma denir. Cebirsel ifadeler çarpanlara ayrılırken farklı yöntemlerden faydalanılır.

1) ORTAK ÇARPAN PARANTEZİNE ALMA

Bir cebirsel ifadeyi ortak çarpan parantezine alarak çarpanlara ayırmak istiyorsak cebirsel ifadedeki her terimde ortak olarak bulunan bir çarpan bulmalıyız. Bu ortak çarpan parantezin dışına yazılır ve parantezin içine de verilen ifadedeki terimlerin ortak çarpana bölümleri yazılır.

ÖRNEK: 3x + 6 ifadesini çarpanlarına ayıralım.

Bu ifade iki terimli bir ifadedir ve bu iki terimde de 3 çarpanı vardır. Ortak çarpan parantezine şu şekilde alırız:

3x + 6 = 3.x + 3.2 = 3.(x + 2)

ÖRNEK: 6x² + 4x ifadesini çarpanlarına ayıralım.

İki terimde de 2x çarpan olarak vardır. Bu yüzden ortak çarpan parantezine şu şekilde alınır:

6x² + 4x = 2x.3x + 2x.2 = 2x.(3x + 2)

ÖRNEK: 4x³ + 12x² − 8x ifadesini çarpanlarına ayıralım.

Bu üç terimli ifadede her ifadede ortak olan çarpan 4x’tir.

4x3 + 12x2 − 8x = 4x.x2 + 4x.3x − 4x.2 = 4x.(x2 + 3x − 2)

$\begin{array}{l} \end{array}$

2) ÖZDEŞLİKLERDEN YARARLANARAK ÇARPANLARA AYIRMA

A) İKİ KARE FARKI ÖZDEŞLİĞİ İLE ÇARPANLARA AYIRMA

Bazı ifadeler Özdeşlik konusunda öğrendiğimiz iki kare farkı özdeşliği kullanarak çarpanlara ayrılabilir. Cebirsel ifadedeki iki terim de eğer tam kare ise bu iki terimin kareköklerinin toplamı ile farkı çarpılır.

ÖRNEK: x²− 25 ifadesini çarpanlarına ayıralım.

x² − 25 = (x − 5).(x + 5)

ÖRNEK: 4y² − 36 ifadesini çarpanlarına ayıralım.

4y² − 36 = (2y − 6).(2y + 6)

B) TAM KARE ÖZDEŞLİKLERİ İLE ÇARPANLARA AYIRMA

Bazı ifadeler Özdeşlik konusunda öğrendiğimiz tam kare özdeşlikleri kullanarak çarpanlara ayrılabilir. Cebirsel ifadedeki birinci terimin karekökü ile üçüncü terimin karekökünün çarpımının iki katı ortanca terimi veriyorsa bu cebirsel ifade bir tam karedir. Çarpanları ise birinci terimin karekökü ile ikinci terimin karekökünün toplamının karesidir (veya farkının karesidir).

x² + 2xy + y² = (x + y).(x + y)

x² − 2xy + y² = (x − y).(x − y)

ÖRNEK: x² + 6x + 9 ifadesini çarpanlarına ayıralım.

İfadesinin ilk terimi x² ve üçüncü terimi 9’dur.

Bu terimlerin karekökleri x ve 3’tür.

Ortadaki terim ise bu kareköklerin çarpımının iki katıdır.

Bu sebeple bu ifade bir tam karedir ve çarpanlara şu şekilde ayrılır:

x² + 6x + 9 = (x + 3)²= (x + 3).(x + 3)

ÖRNEK: 25x² − 20xy + 4y² ifadesini çarpanlarına ayıralım.

İfadesinin ilk terimi 25x² ve üçüncü terimi 4y²‘dir.

Bu terimlerin karekökleri 5x ve 2y’dir.

Ortadaki terim ise bu kareköklerin çarpımının iki katıdır.

Bu sebeple bu ifade bir tam karedir ve çarpanlara şu şekilde ayrılır:

25x² − 20xy + 4y²= (5x + 2y)²= (5x + 2y).(5x + 2y)

4) ax2 + bx + c ŞEKLİNDEKİ İFADELERİ ÇARPANLARA AYIRMA

ax² + bx + c şeklindeki ifadeleri çarpanlara ayırma 8. sınıf müfredatında yer almamaktadır.
Bu şekildeki ifadelerin çarpanlara nasıl ayrıldığını merak ediyorsanız aşağıdaki bölümden öğrenebilirsiniz.

ax² + bx + c üç terimli cebirsel ifade çarpanlara ayrılırken ax2 ve c’nin çarpanları, çapraz çarpımlarının toplamı bx’i verecek şekilde altlarına yazılır. Yazılan çarpanların karşılıklı toplamları verilen ifadenin çarpanlarını oluşturur.

ÖRNEK: x² + 5x + 6 ifadesini çarpanlarına ayıralım.

Bu ifadedeki x² ve 6 ‘yı çarpanlarına ayıralım. Burada ayırırken çarpaz çarpıp toplandığında ortadaki ifadeyi vermesi gerektiğini unutmamalıyız ve ona göre çarpan seçmeliyiz.

x² = x . x ve +6 = 3 . 2 olsun. Burada 6 = (−3).(−2) şeklinde de yazabilirdik ancak ortadaki ifadeye göre seçmek durumundayız.

Üç Terimlileri Çarpanlara Ayırma

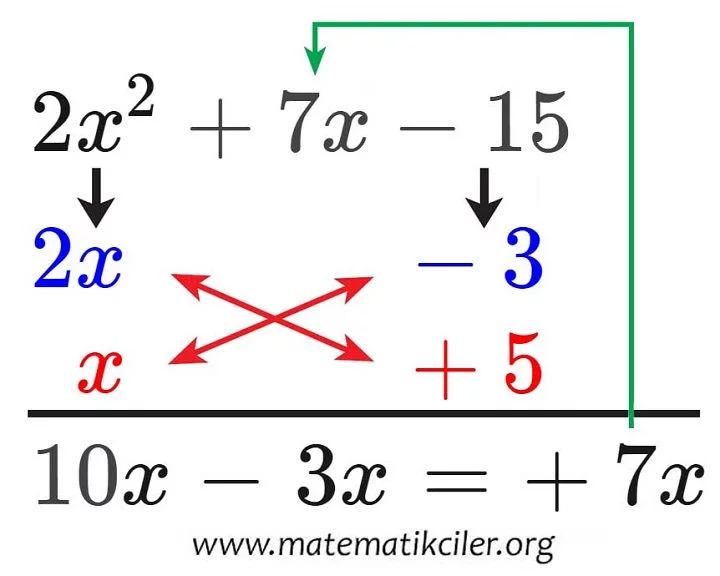
Her iki terimin çarpanlarını altlarına yazdık ve çapraz çarpıp topladığımızda ortadaki terimi vermesini sağladık. Son olarak bu üç terimli cebirsel ifadenin çarpanlara ayrılmış şeklini yazmalıyız. Çarpanlara ayrılmış şeklini yazarken yan yana bulunan ifadeleri toplayacağız ve bunları çarpacağız. Yani resimdeki mavi kısım ile kırmızı kısımı çarpacağız.

x² + 5x + 6 = (x + 3).(x + 2)

ÖRNEK: 2x² + 7x − 15 ifadesini çarpanlarına ayıralım.

Birinci ve üçüncü terimin altına çarpanlarını yazarken uygun çarpanlar seçmeli ve çarpaz çarpılıp toplanınca ortadaki terimi vermesi gerektiğini unutmamalıyız. Buna göre bu ifade şu şekilde çarpanlarına ayrılırdı.

Üç Terimlileri Çarpanlara Ayırma Örnek